

These are complementary Beatty sequences generatedīy and. Here, the zeros occur at positions 1, 3, 4, 6, 8, 9, 11, 12. Spiral, giving a figure known as a whirling square.īased on the above definition, it can immediately be seen that Rectangle into squares lie on a logarithmic
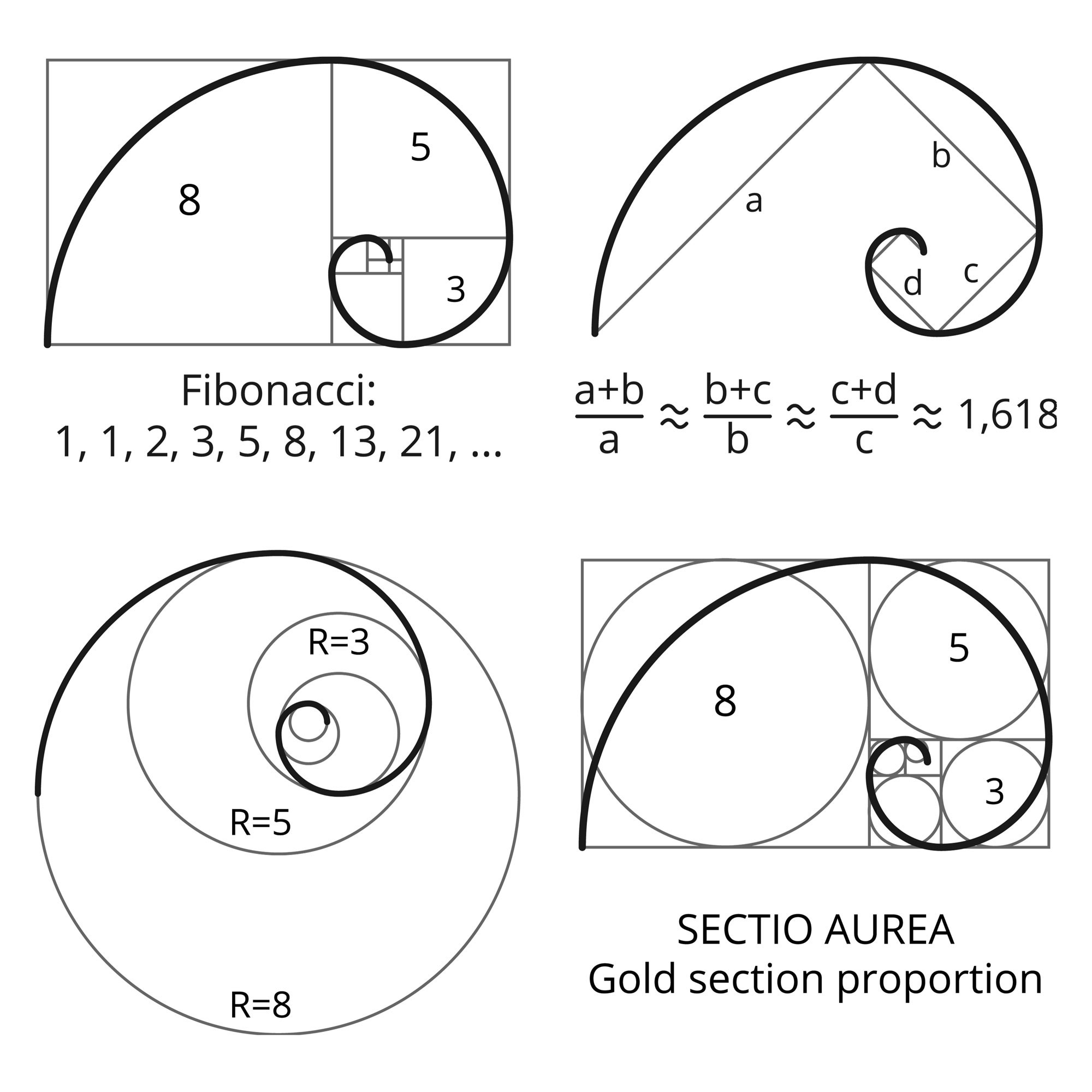
Rectangle, and successive points dividing a golden Is defined as the unique number such that partitioning the original rectangleĪs illustrated above results in a new rectangle whichĪlso has sides in the ratio (i.e., such that the yellow rectangles shown above are similar). Given a rectangle having sides in the ratio , Has surprising connections with continued fractions and the EuclideanĪlgorithm for computing the greatest common However, claims of the significance of the golden ratio appearing prominently inĪrt, architecture, sculpture, anatomy, etc., tend to be greatly exaggerated.
DEFINE GOLDEN SPIRAL CODE
Similarly, the character Robert Langdon in theĭa Vinci Code makes similar such statements (Brown 2003, pp. 93-95). Math genius Charlie Eppes mentions that the golden ratio is found in the pyramids In the Season 1 episode " Sabotage" (2005) of the television crime drama NUMB3RS, Is an abbreviation of the Greek tome, meaning "to cut." Use of the golden ratio in his works (Livio 2002, pp. 5-6). 490-430 BC), who a number of art historians claim made extensive Used by Mark Barr at the beginning of the 20th century in commemoration of the Greek The first known use of this term in English is in James Sulley's 1875 article onĪesthetics in the 9th edition of the Encyclopedia Britannica. The term "golden section" (in German, goldener Schnitt or der goldene Schnitt) seems to first have been used by Martin Ohm in the 1835 2ndĮdition of his textbook Die Reine Elementar-Mathematik (Livio 2002, p. 6). The designations "phi" (for the golden ratio conjugate )Īnd "Phi" (for the larger quantity ) are sometimes also used (Knott), although this usage is The golden ratio, also known as the divine proportion, golden mean, or golden section, is a number often encountered when taking the ratios of distances in simple geometric


 0 kommentar(er)
0 kommentar(er)
